Don’t code before you have conceptualized what you want to code

Binary Search

I am so happy. I have coded binary search from scratch, and this time it feel much much smoother, much quicker even if it was probably the most complex algorithm I have programmed till now.

The main difference is that instead of trying to directly write code, I first of all conceptualized the problem on a word file, and then solved the most complex parts of the algorythm in paper there itslef. Then I only had to pass the code to proper form on the IDE:.

This is how I solved some of the most tricky part. Above you can see what happens when you have an array, and check middle value … how long are the remaining two halfs? This is extremely hard to visualize unless you write it like that. If you do it you realize that, taking advantage of integer division (remainder is lost), you can generalize both halfs to an expression DEPENDING IF the original array is EVEN or ODD.

Below you can also see how I find that integer division can also be used to check if a number is odd or even. This I learned from some of the previous MIT 6.00 classes :). It is great. With integer division you know a number is odd if: (n+1)/2 = n/2 // (remember that in integer division remainder disappears)

And this is how it looked when I passed the code from WORD to my IDE:

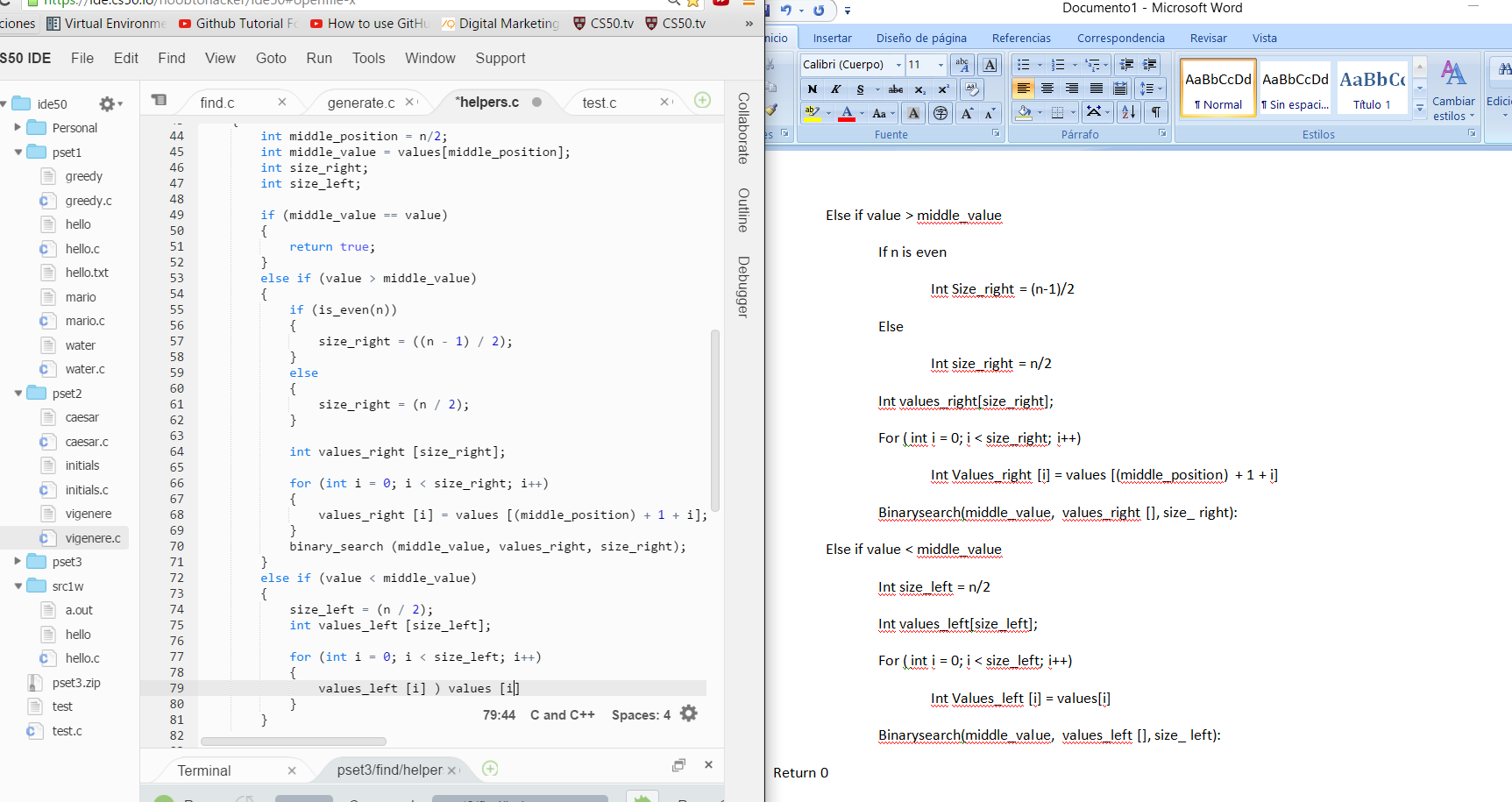
And this is my final code. Enjoy :D!

bool binary_search(int value, int values[], int n)
{
    while (n > 0)
    {
        int middle_position = n/2;
        int middle_value = values[middle_position];
        int size_right;
        int size_left;
        
        if (middle_value == value)
        {
            return true;
        }
        else if (value > middle_value)
        {
            if (is_even(n))
            {
                size_right = ((n - 1) / 2);
            }
            else
            {
                size_right = (n / 2);
            }
            
            int values_right [size_right];
            
            for (int i = 0; i < size_right; i++)
            {
                values_right [i] = values [(middle_position) + 1 + i];
            }
            binary_search (middle_value, values_right, size_right);
        }
        else if (value < middle_value)
        {
            size_left = (n / 2);
            int values_left [size_left];
            
            for (int i = 0; i < size_left; i++)
            {
                values_left [i] = values [i];
            }
            binary_search (middle_value, values_left, size_left);
        }
        
    }
    return false;
}


// Function to check if an integer is even or odd

bool is_even(int n)
{
    if ( ((n + 1) / 2) == (n / 2) )
    {
        return true;
    }
    else 
    {
        return false;
    }
}