How long does a program take to run? Can I improve the speed? How does my CPU affect the speed?

Well, I wrote a program for the MIT course  problem set 1.2 and one thing that caught my attention is that the program, if I run it for a big N, it slows down massively as time goes by, to the extent that it really takes it a long time to reach n = 3000. What if I wanted to calculate for n = 1.000.000? I mean I thought computers nowadays were super fast and all.

So… clearly there must be something hapening and I want to talk about it.

My hypothesis:

• There is a problem with the loops, and I am looping through maybe values that I could avoid looping through.
• Maybe the calculation of logarithm is a difficult one and takes time?
• Maybe the numbers that are being calculated have tons of decimal places or something and really makes the whole thing more complex?
• Current program is printing 3 values every time while executing, maybe this affects?

Why is my computer not using full CPU when I have a long program running in this case?

I have been wondering the following question: When I run a big n, program takes ages to complete… but still CPU usage seems to be only 17% from python… why? Can’t the computer usem ore CPU to complete the operation faster?

Although it is probably more complicated than that… The answer is that my laptop CPU is 4 core. I checked and it is this one i7-6700.

So, very interestingly, 4 cores can’t really run at max all at the same time for the same program unless the program or software you are using is able to do multi core processing. Otherwise it can only use one of the cores. This is why, at max, we can expect 25% being sucked by a program. And the reason why 4 cores sometimes is a good idea is because it allows you to run 2 high intensity programs falwlessly without one interferring the other.

I learned this thanks to this awesome article.

How do I check execution time on python?:

For this I am using Paul McGuire solution HERE.

This will allow us to track execution time of our program.

How much slower is current program becoming as n increases?

I will in this case, try different values of n, and then record the results. (I am sure there must be an automatic way to do this, but its probably too hard, if you know let me know). So I will do it manually. Will run the program many times and note results on an excel.

Also I have run same n = 1280, 2 times and the execution difference was of about 0.1 s over 24s, so we can assume the error due externalities is quite small and negligible.

Result: As you can see in image below, time increases a lot when n increases. For the high n values I saw that more or less the increase in time for n increase was 7 times. So to calculate n= 10000 can take 10 hours and a half!

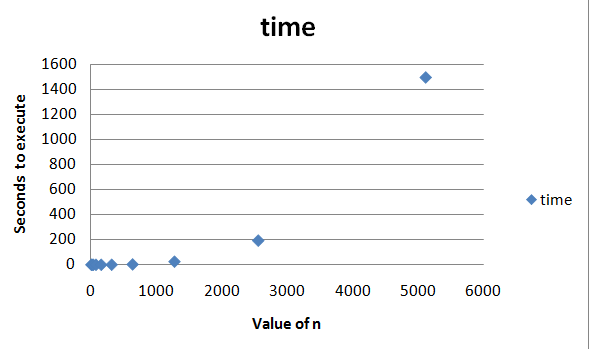
We need to find a way to make the program faster.

How can we make the program faster?

First, does printing value affect the speed of the program significantly?

Program for n = 2560 takes 3 minutes and 15 sec to complete more or less, and prints 3 values every time the first loop re-launches.

Program for n = 2560 without printing anything took pretty much the SAME TIME as while printing values as we went.

Hence printing the end value after each program runs doesn’t really affect the program (As at the end of the day you are only doing “n” printing operations”

However, later I did try to do a test and told the program to print something everytime it did one of the operations in the deepest loop… this means the program had to print much much more that before, and in this case, print executes many many more times than n, and it did affect the speed of the program significantly.

CONCLUSION: Printing takes X time to execute. Obviously if you are telling your problam to print enough big times, then the program WILL slow down.

To make program faster I need to first understand it very well.

I am not that experienced, but I will try.

Basically, first concept is that I am running a program a lot of times, because I want every single value from n to 0 to be printed or saved. Why do I need to run the program so many times? Because everytime the program runs, it calculates for a given N the ratio of the sum of logs of all primes less than N.

The first program I wrote was suitable to find the value of N for 1 value of N only. So if I input n = 200 it will calcualte all primes less than 200 and then find the sum of the log of those.

However, the current program is different. It was meant to produce a list of the results of executing the first program for different values of n. This  means, give me the results of program 1 for n = 200, 199, 198 etc….

And it is doing it in a very inefficient way, because it is basically re-calculating all the primess less than n, every single time when n changes. Instead of that, if I already have calculated the result of n = 200 with the first program, then why should I again find all primes for n = 199? I already know what primes are less than 199, because I had to calculate them to find the solution for n = 200.

If lets say I calculate the sum of logs of primes less than 300, that program already has found all primes less than 300, so if then I want to do n = 100, I should not have to calculate again all the primes less than 100 because I already know them.

Hence, first of all I want to understand how much it takes for the program to calculate just 1 value of n, when N is big. Below the results.

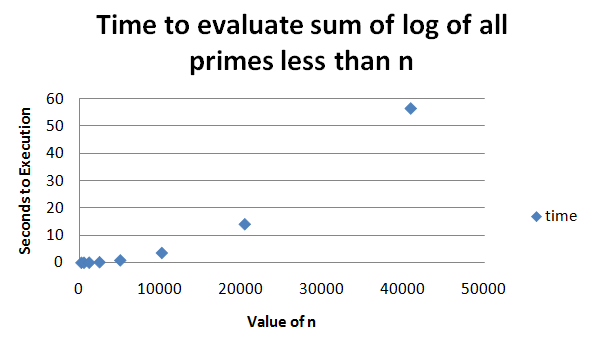
As we see, time it takes is substantially less than the previous, because we are only running program 1 time. This means we SHOULD be able to substantially cut the execution time of the program that prints results for each N value if we build a smarter code that retains the values already calculated so that it doesn’t have to calculate it again. 

Moreover, we can probably optimize even further the root program that we are using to calculate the sum of logs less than n, for a single value of n.

Understanding our current root program fully (this is the basic program that calculates sum of log of all primes less than n, for a given single value of n).

So far the only way I can really understand my program is by adding a lot of “print statements that tell me what the program is doing at each step”. Like below.

 

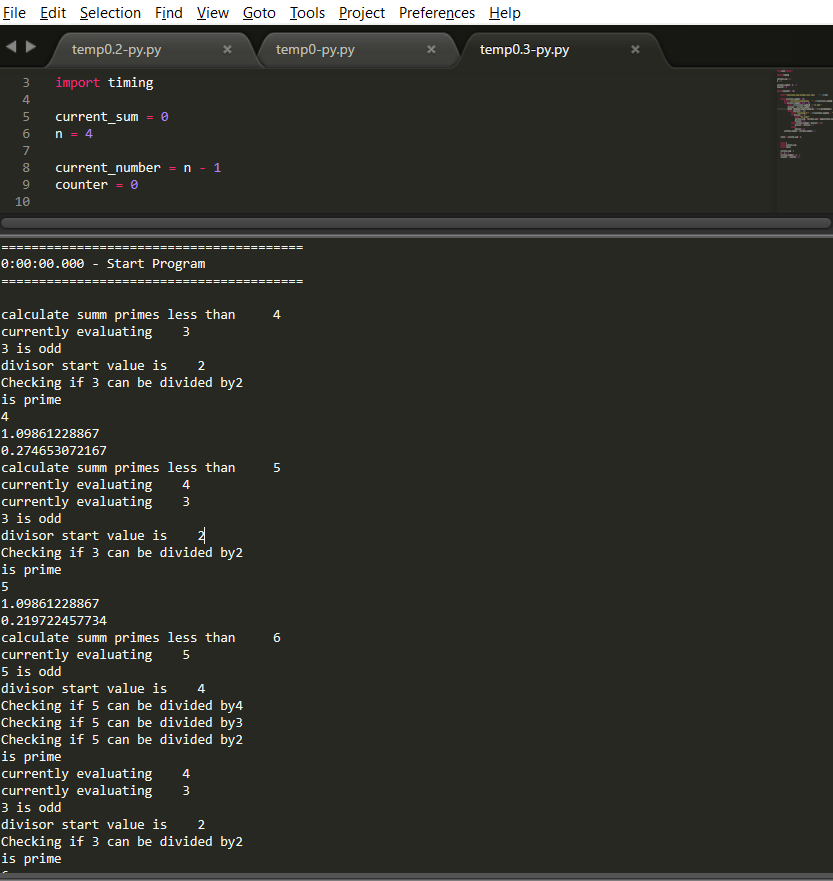
Let’s break down the program. One part checks if a given number is a prime or not by first checking if it’s odd. If it is odd, then it proceeds to divide the odd number into each possible divisor from n – 1 to 1. Here I already can see an issue. If a number is already odd, then when you divide it by an even number, its remainder will always be different than 0, as no odd number divides evenly by an even number.

So I am going to stop checking for those kinds of divisions and will see if this makes a difference. Currently for n = 20480 it takes around 14 secs to execute.
n = 20480
sum of log of primes less than n = 20300.3789022
ratio = 0.991229438582
========================================
0:00:14.063 – End Program

Solving the odd / even division issue

Ok, I have changed the program. Now, when checking if a number is prime, it first checks if it is odd. If it is odd, instead of dividing by ALL possible divisors less than the number, it now ONLY checks all ODD divisors less than the number :).

n = 20480
sum of log of primes less than n = 20300.3789022
ratio = 0.991229438582
========================================
0:00:06.985 – End Program

SUCCESS! Now for n = 20480 it takes around 6 seconds to execute. That means our program is now twice as fast!

Optimizing the program even further

Now discussing the code with a friend, he realized of a VERY important matter. Currently our code, when checking if a number is a prime, it is taking n, and then checking if n / n-1 gives reminder 0, then if n / n -2 gives remainder 0 etc…. Actually, it is much better to start the other way around.

So, if let’s say I want to know if 13 is prime, I won’t do 13/11, 13/9, 13/7 etc…  I will instead do 13/3, 13/5, 13/7…. and this is MUCH more efficient because the program does not need to ever check if a number is for instance divisible by 9… because 9 is 3*3…. so you can already find out if a number is not a prime if it is divisible by 3…

SUCCESS! Now for n = 20480 it takes around 2.3  seconds to execute. That means our program is now three times as fast as the one we optimized before!

Solving the issue of “repeating the same program” many times whenever I want find the result of the first program for many different values of n.

Here we already said that for our long program that gives us the result of the first program for all n values from 0 to n, the time is as follows.

For n = 2560 takes 3 minutes and 15 sec to complete more or less.

Well, after we improved the previous algorithm, now the program takes only 43 seconds! 😀

Obviously because as we saw, the long program all its doing is launching the previous program many times. And we reduced the time the previous took by 7 or 8 times… so this means the long program takes now 7 to 8 times less! This is awesome.

Now the big improvement  for the long program can come from not having to repeat useless operations that we have already calculated. And we should expect the long program to last not much more than when we run the simple first program that only calculates 1 set of results for a single value of n.

(to be continued…)