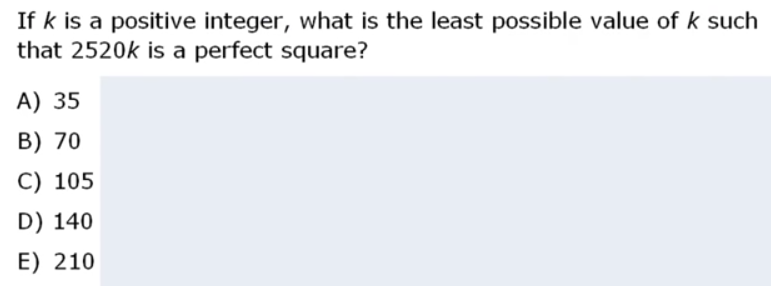Day 2 of GMAT Preparation

Divisibility Rules

I had encounteered these indirectly on my 1st day of review yesterday and DEFINITELY are required in order to solve some questions quickly.

Rules are decently easy to assimilate:

Divisible by 2 if it is even num, divisible by 3 if sum of digits is div by 3, by 4 if num composed of last 2 digits is div by 4, by 5 if ends with 5 or 0, by 6 if div by 2 AND 3, by 9 if sum of digits div by 9, by 10 if ends with 0.

Now, question below took me 1m 56s to solve, which is totally insufficient especially given its easyness. Why it took me so long? Because I didn’t understand the question. I thought the 1) and 2) where the “characteristics” I had to test with or smth, I thought I had to confirm if given that K is positive integer less than 6, then those two conditions match, which is not what is being asked. Those 1 and 2 are actually clues. So basically you know that k is a positive integer less than 6 (ALSO I had to check after but I wondered… is 0 a positive integer? NO. Positive integers are greater than 0), and you know that 3 is a divisor of N, and N is a multiple of 4 (which basically means 4 is a divisor of N).

At about 1min I realized and that’s when I solved it in 56 sec.

Moral of the story… CAREFUL when reading questions. Not pre-assuming things too quickly. Just relax and focus and read what is being asked.

 

 

 

 

Primer numbers

Video suggests memorizing all primer numbers until 59. I am not sure how important is this. I don’t like memorizing. Some important points I learned are:

1. 1 is not a prime number
2. Prime numbers have exactly and only 2 positive divisors
3. 2 is the only even prime number

Instead of memorizing the primes until 59 which again memorizing is very rarely a good idea, I have developed a very interesting exercise. As I know all primes are odd except 2, and I know by heart that 2,3,5,7,11,13 are the first ones… then I just need to quickly keep checking each subsequent odd number, and discard the ones that have obvious extra divisors. I did that very quickly and gave me the list below. Very interestingly I wrote 4 numbers wrong. Numbers I quickly thought were primes but are not, this is SUPER interesting because it shows where my weakness is.

2,3,5,7,11,13,17,19,23,27,29,31,37,41,43,47,49,51,53,57,59

Now, let’s analyze what went wrong:

• 27 – Here I just wasn’t careful. Obviously if I sum 7+2 = 9 hence number is divisible by 3 and 9.
• 49 – Tricky one… as it doesn’t conform with 2,3,5 which are the common ones I look for. 49 is divisible by 7 as it is 7^2. Tricky one indeed and very improtant I don’t make this mistake again.
• 51 – Here I just wasn’t careful, adding 5+1 = 6 so obv divisible by 3. Tricky anyway cause it is 17*3, so that prime 17 messes up a bit the perception that’s why i missed and why it is so important to know the divisibility rules
• 57 – Again, adding digits gives us 12 whcih is divisible by 3. Same case… 19*3, so that 19 prime embedded in the number is what confused me.

Now without looking I will write the list again:

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,51,53,59

Again that careless 51, but much better. Now, what I WILL memorize to make sure I don’t make a careless mistake is that until 59 there are 17 (which is prime!!!) prime numbers. This will ensure I don’t make mistakes again.

Hence if someone asks me, what are all primes till 59, I know it’s 17, and don’t need to use memorizing which is SO unstable and prone to errors. I can just easily deduce it: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59

Doing this exercise prompted the following question: Is there any odd number till 59, whose sum of digits is NOT divisible by 3, and is NOT a prime?

3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59

And the answer is… only: 25,35,49,55 and out of those, it is obvious which ones are divisible by 5, and we know 49 is the only super tricky one. HENCE, one can SUPER quickly and with confidence find all primes till 59 by quickly checking each odd number if it is divisible by 3 or not, (and just making sure the obvious divisible by 5 don’t leak, and that 49 also doesn’t leak). If sum of digits not divisible by 3, then its a prime.

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59

(Also indirectly by doing these exercises I am starting to indirectly memorize the first 8 primes with confidence and without having to think, 2,3,5,7,11,13,17,19.

As a last exercise let me try do it till 100 see what happens:

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,91,97

So it turns out I didn’t do that bad… I doubted about 67, and then I made a mistake with 91. Why? because 91 is not divisible by 3, but again is one of those tricky 7*13 numbers coming from primes. Definitely the table of 7 causes confusion. Almost made a mistake with 77 too but that was easy to spot.

• There are 17 primes till 59
• There are 25 primes till 100.

With this exercise in mind, I am pretty confident about this topic, although it is 80% confidence. I shouldn’t make ANY mistake. Hence it is not yet perfect. But I will keep training it.

Factorization

I love factorization. It is like “de-constructing” a number into its unique components. And this although I knew it more from inutition than from formality is precisely the “prime factorization theorem” that states that any integer greater than 2 is either a prime or can be expressed as a product of prime numbers.

Deconstructing 85 = 5* 17

Deconstructing 36 = 2*2*3*3

etc. This is also the way we find the positive divisors of a number as we analyzed in previous day. So 85 has 4 positive divisors, 36 has 9 positive divisors. I know already without calculating thanks to the formula we learned… Very very careful here, because the formula is a product not sum. So for 36 it is 3*3 not 3+3, I actually made that mistake on the first time. but if you want to test…:

36 – [1, 2 , 3, 4, 6  9, 12,18, 36]

If Y is a divisor of X, then it means Y should be “hidden” somewhere in the prime factorization of X

Next is the exercise below:

 

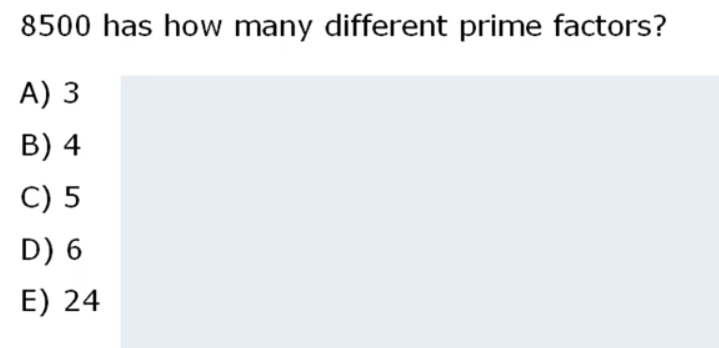
Pretty happy because I solved in 1m 6 sec, and not only solved but said that there are 3 different prime factors, and 24 total positive integer divisors.

Now, obviously I am getting good at this. HOWEVER, I did doubt for a second regarding the wording. It says “How many different prime factors”. The factorization is (2^2) * (5^3) * 17. So what do they mean by “different prime factors”. Well, 2*2*5*5*5*17 hmm… there are 6 total prime factors, out of which 3 uniquely different. Wording is still not 100% clear to me TBH and that is a but annoying, but anyway, luckily I understood correctly. “different prime factors” means that… how many of the prime factors of the number are unique, or different from each other.

Next exercise is below:

I solved it in 2min 10s, not ideal at all… Again, in this case I can see that familiarity with the kinds of questions asked is going to be extremely important. That initial facing the totally unkown makes one waste some valuable seconds.

Now, I did understand the question and proceeded to factorize each number in that 2 to 20 even inclusive range. I made a little mistake and counted 19 “2’s”, when actually there are 18. In any case I chose the right answer as I was confident with the approach, but I need to for sure be careful in each calculation I make because these silly mistakes are exactly what ends up killing me. If 19 had been in the answer choices I’d have had a hard hard time.

Imagine the num was 8, then 2*2*2, then the higherinteger n so that  2^n is a divisor of P would be 3. Keep that in mind too.. because 2^3 is 8 and 8 is a divisor of 8.

Finally, best method to avoid mistakes when factoring? Well… it’s a bit of an advanced topic really, but Ideally if I had infinite time I could devise a strategy. Overall what I am seeing is… if number is big, you wanna make it small asap. Ideally if 10 (2*5) is a divisor, take it down asap using that, also if multiple of 5, do a normal division by 5 to take it down, as otherwise it can be confusing, then take it down by halving it and getting rid of all 2’s and you will probably be left with 3’s and some bigger prime number maybe. Anyway, by doing more and more of these exercises in the future I will anyway be getting better at precision and quickness.

Squares, perfect squares

Squares of integers are also known as perfect squares.

Rule 1: The prime factorization of a perfect square will always have an even number of each prime

Now, I feel this is the kind of thing that is a bit of a “curiosity” but that if one doesn’t know, then if it gets asked, you are screwed. For example If I get asked a question like this (this is another video below ( When I study a topic I like to search different sources for different explanations helps a lot).

Then if you don’t know that rule, you will be in deep trouble. However if you know the rule, then you know very easily than I am gonna need at least one more 7 and one more 5… to make this work, and then add any other pair of primes or different pair of primes to find other numbers. Hence I just need to look at the given possible multiple choice answers (in this case u can’t see in the image but it was 5,70,105,140,350), and then see which one of those has a 7 and a 5, and then pairs of another thing. 140 is the one (7*5*2*2).

RULE 2: A perfect square will always have an odd number of positive divisors

Ok, this is getting a bit ridiculous! XD. Now, having studied pretty well the previous lessons, this makes total sense for sure. if I am always gonna have pairs of factors , then it means that the number of positive divisors will always be (odd) * (odd)* (…) more odds… and when we multiply odd * odd the result is always odd. So, this is quite interesting… because again it shows that, although the concepts are indeed very simple, if one doesn’t actually go through this stuff… then when the moment comes you will be in deep deed trouble if a question is asked that needs this. Currently I have done only 2 days of study and my capacity of retention is pretty ok… for the first time however after hearing this rule, the first little glance of insecurity has come in, thinking… will I be able to remember all these rules? Now, the key is to not be frustrated. Enjoy, enjoy, that’s the whole point. So I am gonna keep enjoy it. I embrace the challenge. Yes, this is awesome… I learned how to quickly factorize, I leearned how to quickly find number of positive divisors of a number, which is so interesting! then I learned that perfect squares have interesting properties such as always having even number of each prime… which then also means they will always have an odd number of positive divisors! 🙂

One question arises… do all numbers that have odd number of total positive divisors are perfect squares?

Well, it actually seems so? DAMN YES! It seems YES! and this is actually a rule that I prefer more than the given one “If a number has han odd number of positive divisors, it is a perfect square for sure” and “All numbers that are NON perfect squares, have an EVEN number of positive divisors”. Ok this is quite exciting actually… I checked the previoys notes where I had factorized number yesterday and yes… it is a great super interesting pattern that was there but I had not realized. Awesome.

Ok another question:

 

So here having properly studied and understood all concepts before, this question becomes VERY EASY. I directly went to factorize 2520 and found out that I was missing 2*5*7 to pair up each factor to make sure I had  a combiantion of even factors each time.

Now, interestingly, it took me 1m 20sec to do it… so even in a situation where a question has become pretty straightfrward, I still take +1m to solve, which is scary and shows how hard it is to respond each question quickly and correctly without mistakes. Now, I truly hope that I will get quicker as time goes by. You will see my progress if you keep following this thread.

Divisor Rules for INTEGERS (important that all num are integers).

Rule 1: For k,M,N as integers, if k is a divisor of N, then k is a divisor of NM

Now even before the video explains why is this the case, I am gonna try answer it myself. I mean… if k is a divisor of N, this means k is a factor of N, this means N, in its components will have k hidden somewhere. Then obviously, if I multiply N by any other integer… k will STILL be inside its components. This makes more sense to me than the rule itself. Basically if a number N has k as one of its divisors, then multiplying N by another integer M, will still have k inside its components no matter what. This seems obvious, I don’t know why they don’t frame things like this instead of complicating it.

Rule 2: given j,k and N are integers, if jk is a divisor of N, then j is a divisor of N and k is a divisor of N

Now, this again same thing. Obviously, if N has j*k in its components… this means N has j in its components, and it means N has k in its components. Pretty clear. So basically if 10 is a divisor of 100, then 5 is a divisor of 100 and 2 is also a divisor of 100. I like to see that, having understood the fundamentals in depth, I am able to really get this pretty quickly.

Rule 3: if k is not a divisor of N then jk is not a divisor of N.

Ok, this wasn’t AS obvious as before but if we think about it it also should make sense. Basically what we are saying is… (btw, it just made total sense, actually is not hard at all), that k is NOT a component of N. Then obviously we know that jk is not a component of N, because for sure k at least is not welcomed in N XD! And the interesting thing is that it doesn’t matter what j is. So for example 3 is not a divisor of 100 (2*2*5*5), hence no matter what you multiply 3 by, it will never be welcomed in N(100). How freaking picky these numbers right? That 3 must be feeling rejected. 🙁 feel sad for it.

Rule 4: if k is a divisor of both N and M then K is a divisor of N+M (and N-M and M-N).

Damn, this sarts getting complex. Ok thought for 2 min and got why even if it is not explained in the video.

Imagine N = 35 (7*5) and M = 21 (7*3). Now, as you can see, 7 is a divisor of 35 and 7 is a divisor of 21, hence the rule says 7 will also be a divisor of (35+21) and (35-21) and (21-35). Why?

Because 35 + 21 = (7*5) + (7*3) which = 7*(5+3), so you can see… no matter what is in the brackets, as both numbers shared 7 as a divisor, the 7 will always be there. So even if it is 7(5-3) or 7(3-5) or 7(3+5), the 7 will always be there.

ALARM SOUNDED 2:30 hours of work till here. I am meeting someone later but wanna do more :D! So I put another alarm of 1:30 hours.

Now, conceptually, what it is important to understand is that, if 2 numbers share the same prime as a factor (so that k number is both a divisor of N and M), then that number will also be a divisor of the addition or substraction of those numbers. Done.

Rule 5: if k is  divisor of N but k is NOT a divisor of M, then k is NOT a divisor of N+M or (N-M) or (M-N)

I was kind of expecting rule 5 to be like this XD! Interesting… hmm… in same previous example, 5 is a fivisor of 35, but not a divisor of 21, so this means that when we do this: 7(5-3) or 7(3-5) or 7(3+5) you can see that… for sure 5 won’t NECESSARILY be a divisor of M… now the rule says it NEVER is. Why… well it is a bit harder to understand but for example:

7(5-3) you can see that if I want to make the brackets end up being a multiple of 5, then that prime factor of M (which in this case is 3) should be either 10, 15, 20, or -10 etc etc… so what I am saying is… if I want the brackets to end up being a multiple of the prime factor of N, then that prime factor of M has to ALSO be a multiple of 5, which is impossible, because we said specifically that 5 was NOT a factor (or a component) of M. That’s why.

Now I understand these concepts but I am a bit scared regarding how to implement these quickly enough. But it’s ok, I am confident. Knowing these concepts will come back once I start actually tackling the problem sets. Let’s see how that goes once I start. But first I wanna study the whole topic.

A great example of why it is actually hard to implement this:

Basically seems a simple question? Took me 1m 30s to conclude that 1) is already enough to know that yes, it is divisible. But then for 2) I wasn’t fully sure if it was sufficient on its own, or if gave any info useful for us. I kind of assumed that if x+y is divisible by 6 then x and y would also be but WRONG. VERY VERY careful.

We said that if k is a divisor of x and k is a divisor of y, then k will be a divisor of (x+y). We DIDN´t say that if k is a divisor of x+y then it must be a divisor of each. For example 4 + 2 = 6. Is 6 a divisor of 6? yes. Is 6 a divisor of 4? NO. and of 2 ? NO. Hence this statement does not really help us at all, it just confuses us. If in doubt, better to try find a case that disproves the statement like above (if one has time). Will keep this in mind. I made a mistake… I shouldn’t make mistakes here. I should be sharper. I will be sharper.

Found also very interesting these different frames of the same question:

You can see they all mean the same. I think I am almost at the point where they all sounds the same to me… maybe 80% there. Need to encounter and do more problems to really interiorize it.

The most counterintuitive one to me is the one “Is there some integer k such that 6k = x”? But then I thought… obviously if X is built by doing 6* (something), then obviously what this means is that 6 must be a factor of X, or a divisor of X.

Greatest common divisors

Now this should be easy. Basically we factorize two numbers and pick all common factors and multiply them together to find the greatest common divisor.

What if there is no prime factor that is common between 2 numbers? Then the greatest common divisor is 1. Again this is something basic but could cause confusion if not studied.

Here an example:

Now this took me 28s to solve. Pretty quickly. As it should be. However as it was so “easy” it did cause a bit of uncertainty in me… did I miss something? etc. Careful with this. I wonder in this situation if it is better to take 20s more to double check, or just move on. We will see as I do more exercises.

Done with this topic. At the end of the day all falls into factorizing and understanding that well. This is just asking what is the max common out of those.

Least common multiple

The least common multiple of integers x and y is the smallest positive integer that has x and y as its divisors.

Again not sure why complicating. This just means that if we have two numbers x and y, the LCM is the smallest number divisible by both, which basically means the smallest number that contains all “components” of both x and y. So if x (2*2*3*7) and y (3*5*13), then what is the smallest number that is contained in both? Well (2*2*3*5**7*13), you can see that both numbers are contained in there. Easy

Interesting to understand “Why” is this important. Well video shows one good example. When we add fractions, we are actually doing LCM under the lines without realizing!

Relation between GCD and LCM

Actually before the video explained it I stopped it and deduced it myself. You can see that if you have 2 numbers for instance 18 (2*3*3) and 42 (2*3*7) then one can see that : GCD * (M/GCD)*(N/GCD) = LCM. This if you simplifie it is equal to : LCM * GCD = L*M

Even and odd numbers and their relationships

Every integer is either even or odd.

1. Even and odd numbers include negative values
2. o is even
3. Even n are divisible by 2 // Even numbers can be expressed as 2k where k is an integer // Prime factorization of even will include at least one 2
4. Odd numbers are NOT divisible by 2 (this is why in a multiplication whenever an even num is involved, the final num is even always).
5. Odd numbers can be expressed as 2k + 1 where k is an integer
6. Odd (+ or -) odd = even  (Makes sense, basically means I am moving on the line of numbers in odd jumps, which will land me on an opposite kind of number)
7. Odd (+ or – ) even = odd (Makes sense, basically means I am moving on the line of numbers in pairs which will of course land me on another odd)
8. Actually although there are rules for 6 and 7, best way is to understand that if I jump odd n of positions  then the nature of my num changes. If I jump even n of positions the nature of the number remains.
9. In multiplication we already said, that as soon as even comes in, will be always even. Only when odd x odd then result is odd.
10. Divison is trickier. EVEN / EVEN can be non integer, even or odd (Makes sense, as it is easy to be EVEN and u can be it even if u have odd components inside)
11. ODD / EVEN – CANNOT be an integer (Makes sense, u can’t split a num with no 2 in its component by 2)
12. EVEN / ODD – not integer, or even (again, it can certainly never be odd, cause that pesky 2 present on numerator will always be there. so it will either be even (when numerator contains some odd that cancel out with the denominator ones) or it will be NON INTEGER, whenever there is no way to fully cancel out those odd nums on denominator.
13. ODD / ODD – basically can be either odd or non integer… will never be even because there is no 2’s to work with

Now let’s see a problem:

 

This is pretty hard. It took me 3m 17s  to get to a wrong answer… which was just because I overlooked something but the approach was right. I guess with practice I’ll improve but I need to be EXTRA careful.

So first important thing is to understand what the sum of 2 componenst can give ODD. Thinking a bit one discovers that only if One component is ODD and one EVEN, then this happens. So on first formula, let’s assume y is the odd component, in that case xy should be even, which can happen if x is even ONLY. If we check other way around, let’s assume Y is even, then xy has to be odd, which is impossible because Y is even and is already there. Hence we are sure X is even. SUFFICIENT.

On second empression, we see a substraction of two components. We know that if result is odd it means that one component is odd other is even. lets assume 6x is odd, well it can’t , so let’s assume 6x is the even then this means x can either be odd or even, and 3y is odd which means y is odd… hence we don’t know if X is actually odd or even from this expression. INSUFFICIENT.

ALARM sounded 1:30 hours went by. Will do 45 min more.

So here the main issue I had was that when considering xy even and y odd, I failed to realize that x MUST be of course even for xy to be even TAKING INTO ACCOUNT Y is odd. That last bit was the main issue. I forgot I knew that Y was odd in that case. Need to be a bit more careful next time.

Very interestingly in the video this is solved in another way:

For expression 1 we turn into y(1+x) is odd. Which means Y is odd and 1+x is odd hence X is even for sure.

But interestingly there is an even further technique that can be used and that I must test for sure each time to understand what is best. This technique is more of a “brute force” one but might actually be the best:

Now let me try this method see how long it takes…. ok it took me 3m 19s but the method gives a lot of certainty and peace. I will have to rehearse more but I think I will end up using this method. Next time I encounter similar problem will use it and see.

Ok this is pretty awesome. Consider this exercise:

I used the table and got an answer 1m 19s, not bad at all. This is very good news, as it really helps simplify the questions. Just need to be careful to understand instead of blindly trust. I like the table technique a lot because in questions where you need to determine what is sufficient or not etc… then you know you are taking ALL cases in consideration. Also, in this case calculations were so easy. Remember we chose 1 for odd and 2 for even. This caused a lot of 0’s in the equation making the calculations super quick. I really like to know that 0 is even and can be used without fear in these kinds of problems. Great.

Properties of consecutive integers

Rule 1: In general every nth number is divisible by n

This means every 6th number is divisible by 6 for instance. Makes sense so far. Now if we have 2 consecutive numbers, this means that one of them MUST be divisible by 2! if we have 3 consecutive we know one of them MUST be divisible by 3 etc.

Rule 2: If we have n consecutive numbers, one of those numbers MUST be divisible by n.

Now here an important issue I just faced. The question is… What conclusions can one take from this expression:

When I saw it, I thought ok let’s simplify by doing n(n^2 – 1). Now, just by doing that I was missing a MASSIVE piece of information which is that (n^2 – 1) can actually be simplified even more to (n – 1) * (n + 1). This is of MASSIVE importance because if I had known, then I’d know we are talking about the product of 3 consecutive numbers…

This is something a bit tricky because we jump into Algebra which is a topic I have not yet revised, and that is very important.

Difference of squares rule

The rule being used here is the “Difference of squares rule”, that says that (a^2 – b ^2) = (a – b) (a + b).  In this case I think because I already learned this in high school long time back, this was stored somewhere in my brain… so now that I see it I will be more careful next time for sure.

Remainders and terminology

Ok so when we divide for instance 15 / 2, we get 7 and 1 remainder. Quocient is the answer to a division problem. Divisor is the number we Divide by, and Dividend sounds like “dividiendo” in spanish which means the number you are diving (in this case 15). Fine, this is clear.

Rule 1: The remainder is always greater than 0 and lower than the divisor (This is super obvious)

Alarm soundedn – 45 minutes passed, actually more, about 1:00 hour I’d say.

I’m back.

Rule2: If N is divided by D, and remainder is R, then possible values of N are: R, D + R, 2D + R etc. 

This is a bit counterintuitive but seems important. Let’s say D is 7 and R is 2, then how can R be  a possible value of N? Well, because 2 / 7  = 0 with remainder 2! Careful with this.

The exercise above is damn easy but took me still 1m 11s… just because I wasn ‘t fully confident. But from division rules we know that if for example 10/3 = 3 and 1 remainder… 3*3 + 1 must equal 10. That’s all the equarion is saying.

I think this concept should be totally fine. If later I encounter a hard question in this regard… then I’ll get worried, but overall seems pretty easy.

Another question:

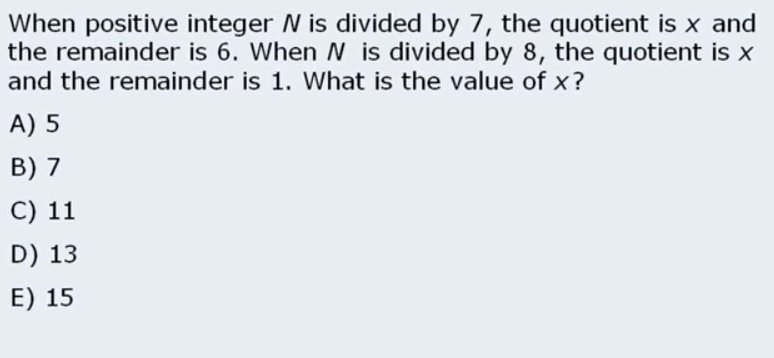
Again super easy hmm… I guess these are the kinds of super easy questions that come at the beginning of the test! Good to know they are not all super hard.

Took me 1m 9s.

Now another interesting question:

This one caught me a bit by surprise to be honest. Took me 2m 11 s to solve which is way too much.

First I tried looking at the equations but got a bit confused, so then changed strategy to just substitute numbers. I tried first with 3, but then when seeing it calculated to 0 I got confused, as I was not sure if 0 is divisible by 6… which it is. (now I learned). Once u go to option D it gives 3, and 3 is NOT divisible by 6. Anyway as I was confused with using 3 which would have been the easier… I chose 15 instead, which gave me the correct answer. D. Clearly its getting late and I am a bit more tired, but glad I got the righr answer anyway.

The other option is to understand that N = x*12 + 3 . (where x is an integer) You can substitute this in each expression, for example on the first it gives 12x. This can be expressed as 6(2x) so yes, it is divisible by 6. On the second expression we get 12x + 18 which again can be expressed as 6(2x+3), which again, it IS divisible by 6 etc etc. 🙂 Proably this method is best, but if a bit blocked, sometimes substituting numbers is best policy.

End of Integer Properties studies

Here I reach the end of the integer properties section of the videos which are being great. I like it so much that I signed up for the free program and will follow it as a foundation: /www.gmatprepnow.com

Overall strategies

Now that I have decided to follow this program first as I feel it is extremely useful and comprehensive, I will start from the beginning. First there is a section about overall strategy which I won’t go into detail unless I encounter problems or truly insightful info. Every problem is a chance to solve and measure so I will take them all. Like this one:

Took me 56s to solve, super easy.

Next one:

Again I think these are just very basic examples to show the kind of questions one can encounter:

And that was also pretty easy. Solved in 59s.  I can totally see Data sufficiency becoming really hard though. Will need to be very careful.

Although Verbal part is absolutely key no doubt, I won’t focus on verbal part in this blog, mainly because overall I am stronger in verbal and I will study that using other means (Like an app ready4GMAT, and then of course videos etc… but won’t coment here). My goal with this is to get all math questions right. Remember the philosophy… if I understand all root concepts well, there is no reason why I shouldn’t answer each and every question right XD! Let’s see what happens.

Alarm sounds 1 hour has passed. Put 45 more minutes.

Timings

This table for timings is suggested. I am not sure if it is the one I will use or how I will manage my time but I wanna keep it for reference here in case I need to go back to it later:

 

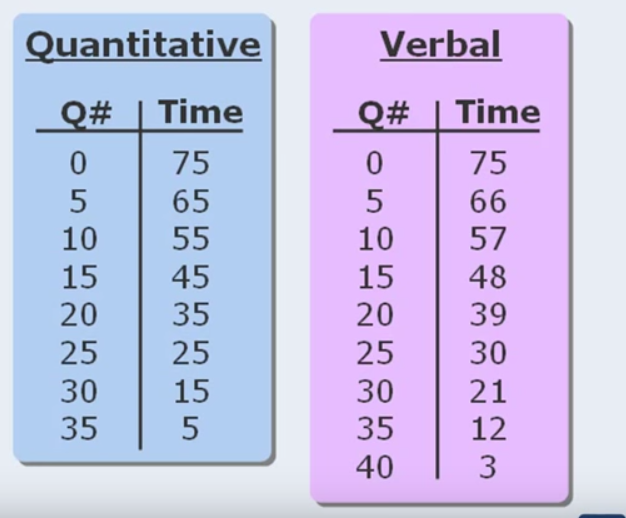In one way or another for sure I must have a strategy to manage my time. We will go into that after I take some full length practice test and see how I manage.

Cancelling score?

I just learned you can cancel your score (which btw you will be able to see right at the end of the exam), and schools wouldn’t know! This is massive really… makes it so much easier if you have enough money to know u can do 2 attempts for example. If in a week I feel confident enough, I might book a test for 3 weeks after now or so… just to see what my true level is… let’s see. Otherwise I plan to take it in Feb or March or so.

Math strategy

This is something I should be good at, but in the question below I performed poorly:

What I did was do the multiplication. Unfortunately I actually forgot how to multiply decimals :S, so I multiplied by 4 first, and then by 15 (result then divided by 100), to get answer d in 1m 2s.

The stupid thing is that… given the answer choices given, I could have estimated D as being the answer much much quicker.

This is another interesting example:

This one I solved better by estimating. So 50% is 412 more or less, and add roughly 50 more so 460 approx which is D. Solved in 15s. But it would have been even more smarter to realize that 50% of 825 is 412,5 which already means D is correct answer FOR SURE.

Now consider this question:

This one I solved in 1m 24s. For some reason this brought a story to my head, something I read years back about a very famous mathematician who got asked this in high school, and found a method to solve it quickly. First u need to determine how many numbers in that range. I don’t remember so I just wrote 1,2,3, and if I do 3-1 then = 2, but actually there are 3 num in that range, so I need to add 1 at the end. Hence 53-12 = 41, so there are 42 numbers in that range, so 2 equally split halfs of 21 numbers.

The smart thing to realize is that if I add the first and last num of the series, it gives me same number than if I add the second and the second last etc… in this case gives 65. So I know that the answer must then be 21*65 = E.

Also I checked answers quickly and saw they are super close together so no estimation could be made.

I am happy to see that even if I forgot everything, still things I might have learnt years back are somehow coming back.

Technique to divide by 5 quickly.

Well, this is handy to know just in case, but basically to divide a number by 5 quickly I can always double the number and then divide by 10 :). Handy technique maybe.

Alarm sounds Ill put 30 min more.

Consider this:

Now again, this I really got blocked and probably solved in 4min or so. Big issues here. First of all I was blocked by the root as i forgot totally how to calculate roots and also how to manipulate them.

What I did was to divide the numebrs into their factors, which helped but eventually missed the whole point. The interesting thing is to realize that both left and right expressions, contain 9 inside of them. So I can re-write them as 25*9 + 9*24. This I could have easily seen just by looking at the factors but I wasn’t sharp enough. Once one knows that then one can do 9*49, which both obviously are perfect squares that I can do root(9) * root(49) hence 3 * 7 = 21

Summary of GMAT Day 2 Study

Conclusion

I did 7 SOLID hours of study today. Hmm… Interesting I thought it had been longer. I should optimize my day better and try to do 9 or so. Let’s see.

I went a lot in depth on proeprties of integers, primes, divisions and some strategy and overall techniques… now I have slight fear I might forget stuff. Let’s not have that fear, let’s enjoy, remember the purpose is to enjoy enjoy, have fun, understand the root concepts, solve problems and crack it. I’ll try to keep enjoying as much as possible.

Big TODO’s

1. Learn how to multiply and divide by brute force using decimals too just in case
2. Learn how roots work and how to solve a root by brute force (maybe)
3. Although on Day 1 I did combinations and permutations, by no means that is mastered and need to come back
4. Although I have done a lot of in depth study on Properties of Integers, I have not done exercises yet, and should probably start doing them asap to test. Need to understand where I can find exercises of this particular kind. If hard then I’ll aim to complete whole Math review ASAP and then I’ll do holstic tests.
5. My main strategy is gonna be following the program diligently and IN DEPTH. I know I might forget something by the end… but it is then that I will start doing a lot of problems, and then going back to each section whenever I feel I have problems. So far this is what I am gonna do.