Finished CS50 Week 3 lectures. Talked a bit about recursion, different sort algorithms… pretty interesting.
Very interesting concept of understanding how long it takes an algorythm to finish depending on show it-s built and the number of values to sort We say, to the order of x. So for example O(n^2) or O(n) or nLog(n).
Seems that divide an conquer is def. better than other sorts because it is Onlog(n) and not n squared, so the bigger n grows, it doesn’t slow down as much as the others (like bubble sort, linear sort or whatever).
Different sort algorithms
Selection sort: Search smallest value on whole array and puts it on first position… etc… takes n^2 worst case. / And in the best case scenario? The same! n^2 !

Bubble sort: Lower value elements shift towards left, higher to the right. Check each pair, and smallest needs to be left, if not swap… after first pass the highest will be on right. You know it is sorted when no swaps happen. In worst case n^2, in best case n!
Insertion sort: First element declare sorted. Then take 1 more, and look at next unsorted element and insert into array sorted. Worst case scenario is n^2, best case is n.
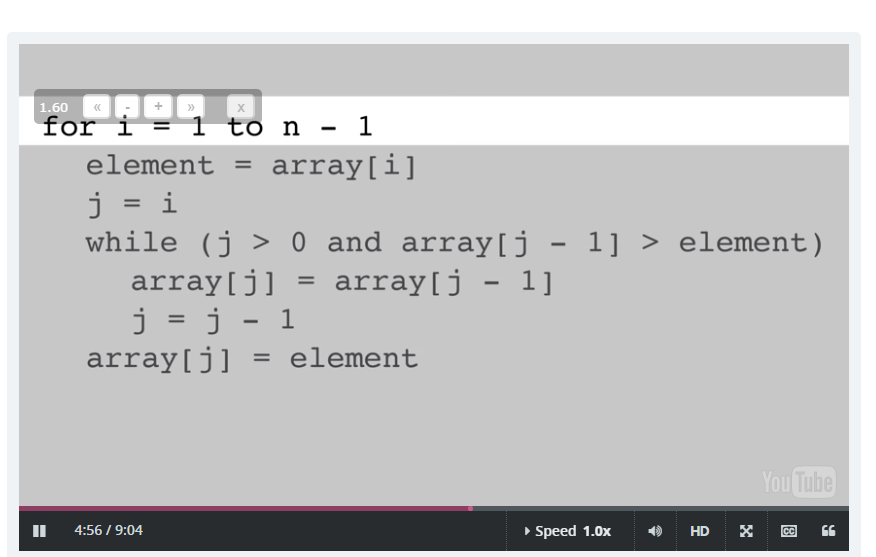
Merge sort: Uses recursion, and basically divides and sorts left side, then right side then merges. Worst case scenario is n*log(n), and best case scenario is n*log(n)?
Different search algorithms
Linear Search: Worst case scenario is n, and best case is 1

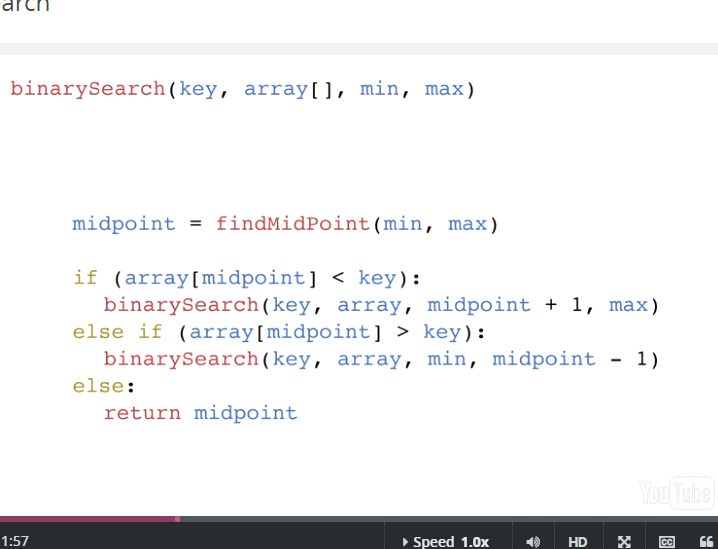
Binary search (for a sorted array): Divide and conquer version of search. Worst case scenario log (n). best case is 1

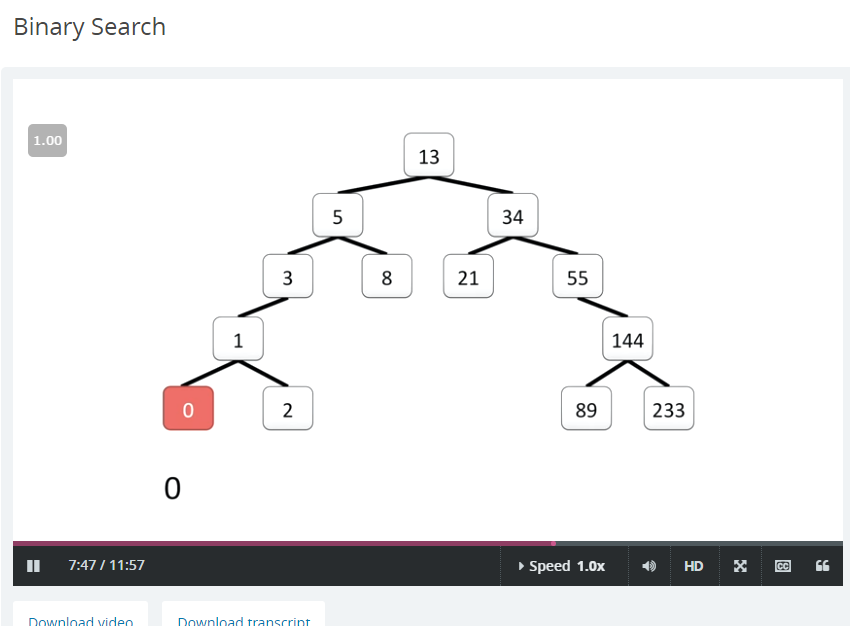
This binary search tree business is pretty heavy. For the moment I think its good enough that I know that it exists, although I would like to understand how it is used and if it is relevant or not… anyway at any point I can go deeper into them,
GDB debugger
Interesting, have not really used it but seems quite helpful to debug. You need to call the environment and then use commands to do different stuff. What I found most interesting is that you might for instance have a program for which the .c file (source code) is missing, and it’s crashing. GDB allows you to investigate, move through the program and still find out what is wrong (in some cases I guess), even if you are not able to really see the source code.